Want to play around with Pi yourself? These programs can help you get started...
Pi in Go
A recent programming language invented by researchers at Google, called Go, is a fun way to play with Pi, because you can write and run short programs online entirely in your web browser using their "playground".
Next, we can use the simple Machin's formula to compute Pi:
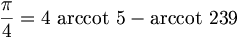
First, we'll do it using native 64-bit floating point math, available in almost any programming language. The program is easy to understand, but note that it only computes Pi accurately to 16 digits!
In order to compute more digits of Pi, we have to turn to Go's support for "big" integers - those larger than 264, or 18,446,744,073,709,551,616. If we were limited to those, we'd only get about 20 digits of Pi, which you could memorize in just an hour. Far too small! Unfortunately, using big number support makes the programs a little harder to read, but it's not too bad. The only thing to remember is that a statement like sum.Div(unity, bigx) sets the value of Sum to be equal to unity / bigx.
- Take a quick look at a program that computes xy using big.Int in go to make this more clear.
Next, we compute the arccot using the taylor series expansion:

- Compute the arc cotangent to high precision using Go - our first step is to define the arc contangent function.
- Using that arccot function, we'll now compute Pi using the basic Machin's formula: Compute Pi in Go using Machin's Formula
- And once you've computed Pi to an interesting number of digits, here's an extension to the above program that counts the number of times each decimal digit (0-9) occurs in Pi
Machin's formula is great, but it's not that fast. A much faster way to compute Pi is to use the Chudnovsky formula. We'll build up to that in bits and pieces. In order to use it, though, we need to be able to compute square roots at high precision, something Go doesn't support natively. Onwards!
For more information about Go, check out their excellent online Go tutorial.
Pi in Py-thon
What better language to play with Pi than one that starts with Py? Nick Craig-Wood has written up a great series of articles about using Python to compute Pi, and the good learning site literateprograms.org offers a few as well:
- Pi in Python using Archimedes method
- Pi with Machin's formula, hosted by literateprograms.org
Machin's formula, invented in 1706, was used to set a new record (see 'why is pi important' for a list of records) of 100 digits of Pi. You can implement it in Python in about 17 lines of code. - NCW implements the Chudnovsky algorithm in Python to compute 100 million digits of Pi, in under 10 minutes. Nice, and with a nice writeup. He also has a more in-depth explanation of the math behind using Machin's formula for Pi.
Pi in many languages
Computing Pi can be useful as a benchmark of computer or program speed - or just fun. Several ways to compute Pi have been implemented in multiple languages if you want to compare across languages:
- Literateprograms has Machin's formula in five languages. This is the same algorithm as the Go version by Dave linked above.
- The Computer Language Benchmarks Game has a pi digits benchmark program in go that's also available in many other programming languages. See how your favorite stacks up!
Playing with math and programs - beyond Pi
If you found some of these examples fun, you should immediately run off and check out Project Euler. Project Euler hosts an increasingly difficult series of problems that you can solve using a mix of mathematical knowledge and computer programming. They're great fun, and you might learn something if you're not careful. I (Dave) personally use the Project Euler problems as a springboard for playing around with new programming languages.