
This calculator calculates how fast you're moving after falling a certain distance — your free fall speed. It ignores friction (air, rock, rope, or otherwise) and relativistic effects: We hope that you won't fall far enough to have either of these make much of a difference! If you fall out of an airplane, however, you'll want to scroll down to terminal velocity. We don't advocate trying to empirically validate these results using your body. Climbing is dangerous. Insert standard disclaimer here.
If you fill in the height, you'll get the time and speed at the end of your fall. If you're kind enough to supply your mass, you'll also get the energy in joules (newton-meters) when you hit the deck. :-) See the plot at the end of the page to see how impact velocity varies with height.
As is probably obvious, the higher you are, the harder you land. The relationship looks like this, in km/h:
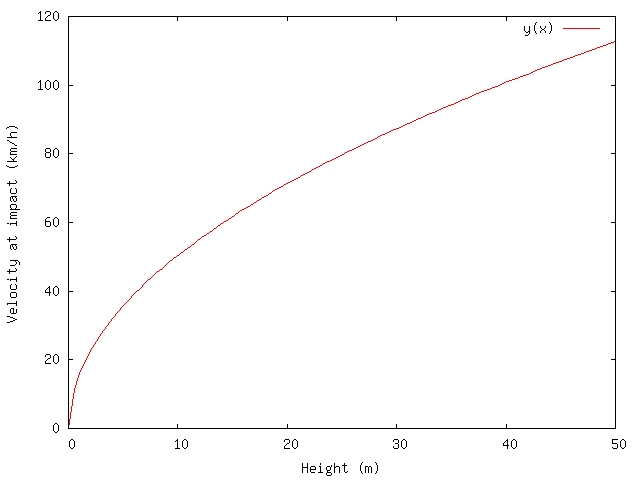
In other words, falling from 50m high is the equivalent of getting hit by a car going 112 km/h, or 70 miles per hour — what would happen if you ran out into a busy freeway. If that's not a decent argument against free soloing, I'm not sure what is.
Free fall / falling speed equations
The calculator uses the standard formula from Newtonian physics to figure out how long before the falling object goes splat:
- The force of gravity, g = 9.8 m/s2
Gravity accelerates you at 9.8 meters per second per second. After one second, you're falling 9.8 m/s. After two seconds, you're falling 19.6 m/s, and so on. - Time to splat: sqrt ( 2 * height / 9.8 )
It's the square root because you fall faster the longer you fall.
The more interesting question is why it's times two: If you accelerate for 1 second, your average speed over that time is increased by only 9.8 / 2 m/s. - Velocity at splat time: sqrt( 2 * g * height )
This is why falling from a higher height hurts more. - Energy at splat time: 1/2 * mass * velocity2 = mass * g * height
Ignoring air friction: Terminal velocity
This calculator doesn't take into account air friction. But think about what happens if you stick your hand out of the window while driving down the freeway: The wind pushes pretty hard against you. That's air friction. The faster you're going, the harder it pushes back. In fact, it pushes back with the square of your speed, whereas the acceleration of gravity is constant. This means that at some point, the force of air against you equals the force of gravity, and you stop accelerating.That point is called terminal velocity (see this wikipedia article for more information). It depends a lot on your position — something shaped like a bullet will have a higher terminal velocity than something shaped like a flat pancake parallel to the earth, because the latter has more surface area exposed to air friction.
The calculator doesn't take any of this into account. In practice, terminal velocity on earth will prevent you from going more than about 320 km/h, or about 200 miles per hour. If you're lying belly-to-the-earth, you'll only travel about 195 km/h (122 miles per hour). As you can see from the graph above, you'd have to fall from higher than 50 meters above the ground for this to really matter much, and at that point, you'd be in enough trouble to not care much. Skydivers, however, should go read the Wikipedia article.
About the calculator
This is a javascript-based calculator. For you history buffs, the
first version used a 10-iteration
implementation of Newton's method
to compute the square root needed for some of the equations, because
in the days of yore, many browsers didn't support sqrt()
natively. You can see the original code here:
newton_sqrt.js - Square root using Newton's
Method in Javascript.
The equations are standard and I verified them, but they're also partly taken from posters on on the old rec.climbing newsgroup — the people who wanted the splat calculator in the first place. Boggles the mind. It's all Clyde Soles fault for suggesting it.
Other Calculators
We've recently added flexible, mobile-friendly compound interest calculators to help evaluate the growth of money, or anything that compounds, over time.
(Disclaimer on the picture: Please, I'm not advocating soloing. I'm actually only about 10' off the deck).